-
MATHEMATICAL ROOTS OF THE DARTS SOFTWARE
DARTS is a hierarchically layered software architecture rooted on
a new approach to modeling of linked multibody systems developed by the
authors, referred to as a spatial operator algebra. DARTS is therefore a
model-based software architecture, in which the underlying mathematical model
for the physical system very efficiently organizes the inherent system
complexity into several layers of mathematical abstraction. The organization
of the software architecture very closely follows that dictated by the
mathematical model. Because this model determines the software architecture,
every software module and computational step has a physical interpretation
which can be obtained by examining the model. The physical relationships
inherent in the system itself provide the software architecture. This features
makes the software architecture very elegant, as this architecture is driven by
an almost overwhelming logic determined by nature, as reflected in the system
mathematical model. Furthermore, the system mathematical model used to
determine the DARTS architecture is itself very efficiently organized by the
spatial operator algebra. One therefore gets the best of two worlds: 1) the
DARTS software architecture is very efficiently organized because it is
model-driven; and 2) the model used to drive the architecture is very
efficiently organized by the spatial operator algebra. The DARTS software is
the embodiment of the spatial operator algebra, and is the spatial operator
algebra reduced to practice, using the principles of modern software
engineering. This algebra is at the root of the elegance and efficiency of the
DARTS software.
[
Return to Top
]
-
THE DOMAIN OF LINKED MULTIBODY SYSTEMS IS VERY LARGE
The Spatial Operator Algebra is a new way to do the mathematics
of arbitrary collections of rigid or deformable bodies connected either by
physical joints or by interactive forces acting at a distance. This domain is
huge. It includes SPACECRAFT, ROBOTS, VEHICLES, ANIMALS, MOLECULES, the SOLAR
SYSTEM, etc. The list is endless. In fact, most of the objects that we
perceive with our ordinary senses in daily life can be viewed as linked
multibody systems. It is difficult to conceive of an ordinary object, or
collection of objects, that cannot be viewed in this way. Other much smaller
systems, such as molecular structures, we cannot experience directly with our
ordinary senses. Special instruments nonetheless reveal their linked,
multibody structure.
[
Return to Top
]
-
THE MATHEMATICS FOR THE DYNAMICAL MOTION OF SUCH SYSTEMS IS VERY
CHALLENGING
Newton said f = ma, force equals mass multiplied by acceleration.
This equation of motion has been at the root of science and technology for
several centuries. It is a very simple equation, as are most fundamental laws
of physics. It is easy to understand and use. In modern times, it is taught
as early as high-school, and even earlier in some schools. However, as
fundamental as it is, this equation needs further elaboration: In its simplest
form, it only governs the dynamical behavior of a fictitious "point" particle
in space that does not occupy any volume. Things are not so simple when
modeling linked, multibody systems. Such systems differ from a "point"
particle in that dynamical interactions between the various bodies in the
multibody system must be accounted for. An example of such a dynamic
interaction occurs when a spinning figure skater contracts the arms in order to
change the speed of rotation. Another important example occurs in space, when
pointing a gimballed camera toward a target may cause dynamic disturbances in
the rest of the spacecraft. This interaction occurs even if the camera is
small compared to the rest of the spacecraft. In some aerospace engineering
circles, this type of interaction is known as the "tail wags dog" effect.
Similar examples occur in all types of linked, multibody systems.
To extend f = ma from a "point" particle to linked multibody
systems, equations of motion must be developed that govern the interactive
behavior of the complete system. These equations are typically very complex.
A significant number of history's greatest scientists and mathematicians have
made definitive contributions on how to develop such equations of dynamical
motion. Euler, Lagrange, and Hamilton are among the most prominent. The
science they created is classical mechanics, which governs the dynamical motion
of most ordinary events when viewed at an ordinary human scale. Relativity and
quantum mechanics were revolutions which came later.
[
Return to Top
]
-
MATHEMATICAL COMPLEXITY IS OVERWHELMING EVEN FOR RELATIVELY
SIMPLE SYSTEMS
A simple robot with 6 articulated joints and 6 rigid links is one
of the most common tools for robotics applications and research throughout the
world. Fig. 1 displays the complexity of the corresponding equations of
motion. There is an overwhelming proliferation of mathematical symbols and
trigonometric functions (Sine, Cosine, etc.) of the various joint angles.
There are also many subscripts. Counting the number of symbols is an
overwhelming exercise, even without trying to comprehend what the symbols mean.
There are so many trees that one cannot see the forest.
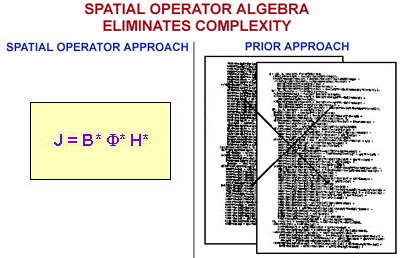
Figure 1
[ Back to Section IV
|
Back to Section V ]
Complexity gets even more out of hand for more complex systems.
Some of the applications mentioned above (molecular structures, animals, etc.)
have significantly many more degrees of freedom than a simple robot. Unless
the equations of motion for such systems are organized efficiently, the
mathematical complexity may be far beyond human capabilities.
[
Return to Top
]
-
THE SPATIAL OPERATOR ALGEBRA ELIMINATES COMPLEXITY
The Spatial Operator Algebra is a new approach to the mathematics
of linked multibody systems. One of its key innovations is that it eliminates
mathematical complexity. It reduces the number of symbols that a human analyst
must see and understand by several orders of magnitude. This is done by using
such spatial operators as f and H in Fig. 1, with each operator symbol
representing up to 10,000 more detailed arithmetical operations. Fig. 1
compares the extremely simple mathematical expressions prevalent in the Spatial
Operator Algebra and the corresponding very complex expressions in prior
approaches.
While complexity is eliminated, no information about the system
is lost in the Spatial Operator approach, as the spatial operators still
contain precise information about the system. However, this information is
organized and presented to the analyst using much fewer symbols.
Complexity is reduced to what may be the absolute minimum. Even
very complex systems require only a few spatial operator symbols. It is
difficult to conceive how there could ever be a simpler mathematical
representation.
[
Return to Top
]
-
COMPUTATIONAL COMPLEXITY GROWS ONLY LINEARLY WITH THE NUMBER OF
DEGREES OF FREEDOM
Each spatial operator in the Spatial Operator Algebra is
mechanized by an algorithm requiring arithmetical operations which grow only
linearly with the number of degrees of freedom. These are known as "Order N"
algorithms, because the number of arithmetical operations is of the same order
as the number N of degrees of freedom. This means that, as system complexity
grows, computational complexity grows only linearly. This is almost ideal. It
would be absolutely ideal if the number of computations did not grow at all
with system complexity, but this may not be possible. However, the Spatial
Operator Algebra comes close to this. This is particularly true, because in
most traditional methods, the number of arithmetical operations grows as the
cube of the number of degrees of freedom. Fig. 2 shows a comparison, in terms
of the number of arithmetical operations required, between the Order N
algorithms embedded in the Spatial Operator Algebra and the Order N-Cube
algorithms of prior state of the art. The Order N algorithms in the Spatial
Operator Algebra are referred to in Fig. 2 as NEIMO, which stands for Newton
Euler Inverse Mass Operator method.
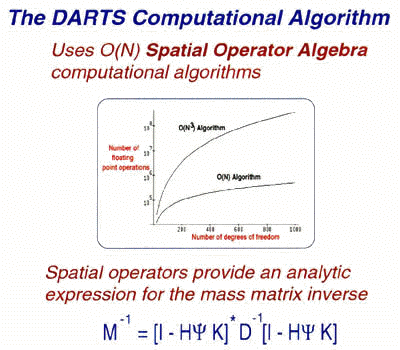
Figure 2
[ Back to Section VI ]
[
Return to Top
]
-
THE SPATIAL OPERATORS EXTEND TO 3-DIMENSIONAL MECHANICAL SYSTEMS
THE COMPUTATIONALLY EFFICIENT DIGITAL FILTERING TECHNIQUES OF
MODERN SIGNAL PROCESSING
Each spatial operator in the Spatial Operator Algebra is
implemented using a spatiallly recursive algorithm, in which the necessary
computations are performed in a sequential series of steps. Each sequence
starts at one end of the system and terminates at the other end. Many of the
spatial operators, those requiring inversion of the system mass matrix for
example, are mechanized by spatially recursive Kalman filtering algorithms,
quite popular in digital filtering and signal processing. Since it was
announced by R. E. Kalman, now at the University of Florida, in the early
1960's, his Kalman filtering algorithm has found its way to countless
applications in science and engineering: aerospace navigation, guidance and
control; satellite orbit determination; digital image processing; stock market
modeling and prediction; weather forecasting; etc. It has been stated in some
occasions that a good metric to measure the relative state of advancement of a
society is the number of Kalman filtering applications in this society. While
this claim may have been made somewhat in jest, it may not be far from the
truth.
That the Kalman filter embedded in the Spatial Operator Algebra
solves computational bottlenecks in classical mechanics is a very surprising
scientific discovery, requiring a deep understanding of both classical
mechanics and filtering methods.
[
Return to Top
]
-
THE SPATIAL OPERATOR ALGEBRA EMERGES FROM A SYNTHESIS OF SEVERAL
SCIENTIFIC DISCIPLINES, PREVIOUSLY THOUGHT TO BE UNRELATED
The Spatial Operator Algebra solves problems in classical
mechanics using a combination of powerful methods previously thought to be
unrelated to mechanics: (1) Filtering and Prediction Methods, which emerged
initially during World War II to address problems in predicting the future
trajectories of missiles and other projectiles. N. Wiener, the father of the
term Cybernetics, was among the most prominent founders of this scientific
discipline; (2) Functional Analysis and Linear Operator Methods, a unifying
mathematical framework used widely in engineering and science (for example in
quantum mechanics); (3) Linear Control System Theory, which has enabled the
design of digital automatic control systems in many space and terrestrial
applications.
Finding previously undiscovered relationships and analogies among
areas is one of the most fundamental contributions that can be made. Such
discoveries inevitably enhance our knowledge and understanding of the areas
synthesized. For example, efficient computational techniques, which have
emerged from about 50 years of intensive research in Filtering and Prediction
Methods, can now be used to organize complexity and solve computational
bottlenecks in classical mechanics. Knowledge from any given area is applied
to previously unresolved problems in the other areas. Finding analogies and
relationships therefore fills in gaps in our knowledge, and it advances
knowledge in all related areas. To a large extent, the Spatial Operator
Algebra does this.
[
Return to Top
]
-
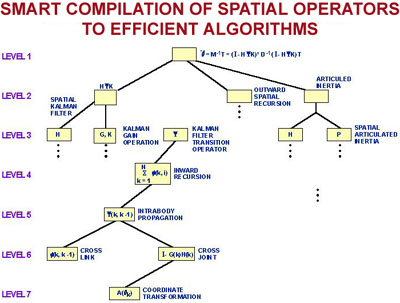
THE SPATIAL OPERATOR ALGEBRA LEADS TO A HIERARCHICAL SOFTWARE
ARCHITECTURE BUILT FROM STANDARDIZED, REUSABLE MODULES
The Spatial Operator Algebra is easily implemented using modern
software development methods. At any given level in the hierarchy, the
computer automatically decomposes each spatial operator into a set of a few
more detailed operations at the next lower level in the hierarchy. There is a
corresponding decomposition in the software architecture. This process of
decomposition can be viewed as that of "smart" compilation, in the sense that
the compiler is made smart by built-in knowledge about the system dynamical
model embedded in the spatial operators. The software modules which constitute
the architecture are simple, standardized, and easily debugged.